小学数学奥林匹克竞赛模拟题第一部分第二节

二、有规律的数列

习题二

1、找出以下各个数列的规律，在括号里填上适当的数。

(1)3，12，27，48，75，( )；

(2)3，26，111，324，755，1518，2751，( )；

(3)2，10，10，66，26，218，50，514，82，1002，( )，( )；

(4)0.25，0.4，0.5，1.6，0.75，3.6，1，6.4，( )，( )。

2、239被某数除，所得的商与除数相同，余数比除数少1，求出余数来。

3、在一个两位数的两个数字中间加一个0，那么所得的3位数是原数的7倍，求这个两位数。

4、一个两位数，把它的个位数字与十位数字交换位置后所得的两位数比原数多18，求出这个两位数来。

5、由算式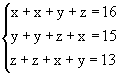，求出x，y，z代表什么数。

6、六年级有甲乙丙丁4个班，不算甲班，其余3班一共有147人，不算丁班，其余3个班共有144人，乙丙两班人数之和与甲丁两班人数之和相等，求4个班共有多少人？

7、计算下式的值：

　　(1++++)×(++++)-(1+++++)×(+++)。

8、(第7题的推广)设n≥3是一个自然数，计算下式的值：

　　(1++…+)×(++…+)-(1+++…+ +)×(+…+)。

9、有9个不同的自然数，从小到大排成一行，相加的和为61，如果去掉其中最小的和最大的数，剩下7个数的和是49，求在原来排列的次序中，第三个数是多少？

10、计算。

11、一个分数在约分前分子分母的和为108，如果分子加上15，分母加上12再作约分，恰好得到，求原来的分数化成最简分数应是多少？

12、连结圆周上任意两点的线段叫做弦，直径正好就是经过圆心的弦。一个圆被一条直径和一条弦划分，最多可分成4个区域。一个圆被2条直径和一条弦划分，最多可分成7个区域。那么，一个圆若被一百条直径和一条弦来分，最多可分成多少个区域呢？

13、3个三角形最多可把整个平面分成多少个区域？4个三角形呢？10个三角形呢？

14、仿照例6的方法计算1³+2³+3³+…+n³。

15、10条直线最多可以把平面分成几部分？

习题二提示及部分解答

1、(1)仿例1(1)题的方法即可；(2)反复用例1(1)题的做法，直到找出规律为止；(3)这是由两个数列凑合而成的，对每个数列用上述方法；(4)它也是由两个数列合成的，做法与上一小题同。

2、解法一：因为商与除数相同，所以商与除数的乘积是一个平方数，而且这个平方数一定不超过239(想一想理由是什么？)。然后判断不超过239的平方数中，哪个平方数是符合题目要求的(这里要用到除法中除数与余数的大小关系)。由此即可求出除数。解法二：设除数是x，那么根据条件，并把除法改用乘法(想想怎样用乘法对除法作验算)写出来就可得到239=x²+x-1。等式两边都加1得239+1=x²+x，这就是x(x+1)=240。把这个式看成是两个连续自然数的积是240，你应该知道怎样求x了。

3、设这个两位数为ab，a是十位数字，b是个位数字，那么这个两位数可以写成10a+b。同理，中间加一个0所得的3位数可以写成100a+b。于是由题给条件可列出下面的式子，100a+b=7(10a+b)，从而100a+b-b-70a=70a+7b-b-70a，这就是30a=6b，因此b=5a。注意到a、b只能取小于10的数即可求出它们的值。

4、注意两位数ab与ba分别可表示成10a+b以及10b+a，然后按题意列式求解。

5、这种几个字母轮换出现的式子通常用加法去做，即把3个式子的左边和右边分别相加，这就得到4x+4y+4z=44，由此即可求出x+y+z的值。

6、根据条件列出以下式子：

　　

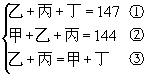
由①，②两式推出丁=甲+3，代入③式得

　　2甲=乙+丙-3 　　④

把②式两边都乘以2得

　　2甲+2乙+2丙=288　 ⑤

用④式代替⑤式中的2甲，就可求出乙+丙的值。再利用③式就可求出四班人数总和。

7、算式里有4个括号，4个括号中共同有的是+++，就设a=+++，题目中的式子就变成(1+a)×(a+)-(1+a+)×a，利用分配律两次(参考(2.8)式的计算过程)就可以算出它的值。

8、做法与上题同，只不过这次应假设a=+…+，于是原式变为(1+a)×(a+)-(1+a+)×a。

9、注意其中最小与最大的两个数的和是61-49=12。由此再利用2+3+4+5+6+7+8+9+10=54比61小推出，最小，最大两数只可能是1和11。最后注意1+2+3+4+5+6+7+8+9+10+11=66。剩下的推理由你自己完成。

10、此题与第7、8两题类同，千万不要直接计算。注意到分子、分母中四个数的共同点，可以设a=，于是原式变为，用分配律把分母的值算出来即可。

11、假设约分前分子为a，分母为b，那么由题意得到

　　a+b=108　　　 (1)

　　= 　　(2)

注意到(2)式就是b+12=2×(a+15)，即有b+12-2a-12=2a+2×15-2a-12，这就是

　　b-2a=18。　　 (3)

(1)式表示a与b的和是108，而(3)式表示b比a的2倍还多18，现在求a，b就容易了。

12、解法一：先研究3条直径和1条弦最多可把圆分成几个区域，结论是10个，再由数列4，7，10，…的规律求出问题的答案。

　　解法二：先考虑一百条直径把圆分成多少个区域(注意每加一条不同的直径，划分的区域多出2个)，然后再添上一条弦，看它能增加最多多少个区域。

13、注意先研究一个及两个三角形的情形。方法与上题类似。

14、先证明对任何自然数n有

　　(n+1)⁴=n⁴+4n³+6n²+4n+1，　(1)

由此推出

　　(n+1)⁴-n⁴=4n⁴+6n²+4n+1。　(2)

然后利用(2)式分别取n为1，2，…，n-1，n得出n个等式。把这些等式左、右两边分别相加，然后利用(2.15)式及关于前n个自然数的和的公式就得出要求的计算公式了。详细过程参见例6。

　　另解：此题还有一个特殊的解法。直接计算可得

　　1³ 　 =1²；　 1³+2³ 　　 =3²；

　　1³+2³+3³ 　　 =6²；　1³+2³+3³+4³=10²；

　　1³+2³+3³+4³+5³=15²；

　　… … … …

　　注意到数列1，3，6，10，15，…， 　(1)

它的规律是：其中第n个数等于1+2+…+n，即可得出

　　1³+2³+…+n³=(1+2+…+n)²=()²。　(2)

在寻找数列(1)中第n个数的规律时，仍然要用到正文中例1给出的方法，即把(1)写成

　　

并注意3=1+2，6=1+2+3，10=1+2+3+4，15=1+2+3+4+5等等。

15、仿照例3或习题第13题。