加法原理

　　22 两次投掷一枚骰子，两次出现的数字之和为偶数的情况有多少种？

　　23 从 1～ 9中每次取两个不同的数相加，和大于 10的共有多少种取法？

　　24 大林和小林共有小人书不超过50本，他们各自有小人书的数目有多少种可能的情况？

　　25 从2，3，4，5，6，10，11，12这七个数中，取出两个数组成一个最简真分数，共有多少种取法？

　　26 在下列各图中，从A点沿实线走最短路径到B点，各有多少种走法？

　　27 在左下图的街道示意图中，C处因施工不能通行，从A到B的最短路线共有几条？

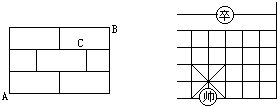
　　28 如右上图，象棋盘上一名小卒过河后沿最短的路线走到对方“帅”处，有多少种不同的走法？

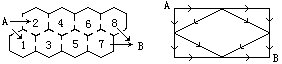
　　29 如左下图，从A处穿过房间到达B处，如果要求只能从小号码房间走向大号码房间，那么共有多少种不同的走法？

　　30 沿右上图所标的路径和箭头所指的方向从A到B共有多少种不同的走法？

　　31 有一楼梯共10级，规定每次只能跨上一级或两级，要登上第10级，共有多少种不同走法？

　　32 有一楼梯共10级，规定每步跨上两级或三级，要登上第10级，共有多少种不同走法？

　　33 有一堆火柴共 12根，如果规定每次取 1～3根，那么取完这堆火柴共有多少种不同取法？

　　34 某工作需要钳工2人和电工2人共同完成。现有钳工2人、电工2人，另有1人钳工、电工都会。从这5人中挑选4人完成这项工作，共有多少种不同选法？

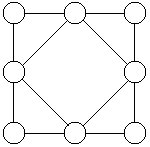
　　35 将右图中的○分别涂成红色、黄色或绿色，要求有线段相连的两个相邻○涂不同的颜色。共有多少种不同涂法？

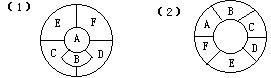
　　36 分别用五种颜色中的某一种对下列各图的A， B，C，D，E，F六个区域染色，要求相邻的区域染不同的颜色。问：各有多少种不同的染法？

　　37 在右图中，从A点沿线段走最短路线到B点，每次走一步或两步，共有多少种不同走法？（注：路线相同步骤不同，认为是不同走法。）

　　38 游乐园的门票1元1张，每人限购1张。现在有10个小朋友排队购买，其中5个小朋友只有1元的钞票，另外5个小朋友只有2元的钞票，售票员没有准备零钱。10个小朋友排队，不同的排队方法共有10！=种。问：其中有多少种排队方法，使售票员总能找得开零钱？