五 智巧问题

　　1 某国的货币有1元、50分、20分、10分、5分、2分、1分共七种硬币（1元=100分）。某人带了9枚硬币去买东西，凡不超过2元的东西他都能拿出若干枚硬币支付，钱数正好，无需找钱。这9枚硬币的总面值最多是多少？最少是多少？

　　2 A，B，C，D四人进行围棋比赛，每人都要与其他三人各赛一盘。比赛是在两张棋盘上同时进行，每天每人只赛一盘。第一天A与C比赛，第二天C与D比赛，第三天B与谁比赛？

　　3 有20间房子，有的开着灯，有的关着灯。在这些房子里的人都希望与大多数房子保持一致。现在，从第1间房子里的人开始，如果其余19间房子的灯开着的多，就把灯打开，否则就把灯关上。假设最开始时开灯与关灯的房子各10间，并且第1间房子的灯开着。那么，这20间房子里的人轮完一遍后，开着灯的房子有几间？

　　4 甲、乙、丙三名选手参加长跑比赛。起跑后甲处在第一的位置，在整个比赛过程中，甲与乙、丙的位置次序共交换了7次。比赛结果甲是第几名？

　　5 正义路小学共有1000名学生，为支持“希望工程”，同学们纷纷捐书，有一半男生每人捐了9本书，另一半男生每人捐了5本书；一半女生每人捐了8本书，另一半女生每人捐了6本书。全校学生共捐了多少本书？

　　6 某杂志每期定价1.50元，全年共出12期。某班部分同学订半年，其余同学订全年，共需订费720元；如果订半年的改订全年，订全年的改订半年，那么共需603元。问：这个班共有多少名学生？

　　7 某次猜谜语比赛，谜语按难易分两类，每人可以猜三条。每猜对一条较难的谜语得3分，每猜对一条较容易的谜语得1分。结果有8人得1分、7人得2分、6人得3分、5人得4分、4人得5分。恰好猜对两条谜语的有几人？

　　8 一排六棵树（见下图）分别是六个人栽的，A，B，C三人栽的是大树，D，E，F三人栽的是小树。如果A与E栽的树相隔两棵树，B与F栽的树相隔一棵树，那么C栽的树是左起第几棵？

　　9 一个正方形大厅被分隔成16个小间（见右图），每相邻两间都相通，有阴影的四间是休息室，其余布置成展览室。从A处出发，使走过的房间数最少而到达休息室（可以是任何一间）的不同走法共有多少种？

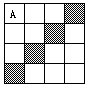
　　10 整盒香烟在盒中排列如左下图所示。抽出2支香烟后（右下图），剩下的香烟在盒中仍不能移动。要保持剩下的香烟在盒中仍不能移动，最多能抽出多少支香烟？

　　11 有一根长8m的方木，锯成等长的5段，表面积增加了1m2，求这根方木的体积。

　　12 生物学家发现一种胞子，每小时可分裂成3个，每个新胞子同原来的一样，一小时后它们中的每一个又都可以分裂成3个。这种过程连续不断地进行下去。一天早晨，一位生物学家在一个容器中放入一个胞子，到了中午

　　13 兔子和乌龟在一个200米的环形跑道上赛跑，它们从同一地点同时出发，乌龟每爬行5米，兔子超过它1圈。当乌龟爬完1圈时，兔子跑了多少圈？

　　14 兔子跑3步的时间狗跑2步，兔子一步跑1米，狗一步跑1.5米。如果狗和兔子在100米的直跑道上赛跑，赛程为一个往返，狗和兔子调头的时间相等，那么谁将获胜？

　　15 有一口枯井深10米，一只蜗牛从井底向上爬，白天向上爬3米，晚上向下滑2米。问：这只蜗牛几天能爬出井？

　　16 某学校进行乒乓球单打比赛，参赛选手共56人。如果采用淘汰赛，最后产生一名冠军，那么一共要比赛多少场？

　　17 有六条铁链，每条有四个环（见下图）。已知打开一个环要用5分钟，闭封一个打开的环要用7分钟。现在要把六条铁链连成一条长铁链，至少要用多少时间？

　　18 从分别写有3，4，5，6，7，8的6张卡片中任取三张，做三个一位数的加法，问：可能得到多少种不同的结果？

　　19 一个玩具上有红色和白色按钮各一个，还有100个能站能坐的小木偶，按一下红色按钮就会有一个小木偶坐下，按一下白色按钮就可以使站着的小木偶增加一倍。现在只有两个小木偶站着，要想使站着的小木偶增加到27个，最少按几次按钮？怎样按？

　　20 箱子中放着一些茶杯，有一个小朋友从箱子里往外拿，每次拿出箱子里茶杯总数的一半，然后再放回一个。拿了100次之后，箱子里还有两个茶杯，求开始时箱子里的茶杯数。

　　21 某商店规定3个空汽水瓶可以换一瓶汽水，小明有10个空汽水瓶。问：他一共可以换到多少瓶汽水？

　　22 红、蓝墨水各一瓶，用一根滴管从红墨水中吸一滴滴到蓝墨水中，搅拌后，再从蓝墨水中吸一滴同样体积的墨水滴到红墨水中。这时红墨水中的蓝墨水多，还是蓝墨水中的红墨水多？

　　23 足球队有18名队员，其中10人穿大号球衣，8人穿小号球衣。小马虎将10件大号球衣和8件小号球衣领回来后，一人一件地随便发给了每个队员，结果有的大个队员领到了小号球衣，小个队员领到了大号球衣。问：大个队员领到了小号球衣的人数与小个队员领到了大号球衣的人数哪个多？为什么？

　　24 50名同学面向老师站成一行。老师先让大家从左至右按1，2，3，…依次报数；再让报数是4的倍数的同学向后转，接着又让报数是6的倍数的同学向后转。问：现在面向老师的同学还有多少名？

　　25 用铁丝制成左下图的铁丝网，重量是30克。用同型号的铁丝制成右下图的铁丝网，重量是多少克？

　　26 某幼儿园的孩子中，任意5个孩子的年龄之和不大于20，所有孩子的年龄之和是140。这个幼儿园至少有多少个孩子？

　　甲杯里的水还剩多少克？

　　：甲、乙二人谁分到的蛋糕多？

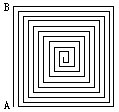
　　29 右图中AB的长度是20cm，任意相邻两圈的距离都是1cm。求图中所有线段的长度和。

　　30 六年级一班有20个男生，某次考试全班有24人超过90分，问：女生中超过90分的比男生中未超过90分的多几人？

　　31 小明的左衣袋和右衣袋中分别装有相同数目的硬币，两衣袋中硬币总钱数也相等。当任意从左衣袋取出两枚硬币与右衣袋的任意两枚硬币交换时，左衣袋的钱数要么比原来多二分，要么比原来少二分。问：两个衣袋共有几分钱？

　　32 一个人买了D元C分钱的商品（C为一位数或两位数），交给售货员20元钱，售货员错误地看成C元D分，于是找给买主4.88元。按正确的价格，售货员应找给买主多少钱？

　　33 爸爸有一个储钱罐，里面放的都是五分的硬币。爸爸清点时发现，硬币的枚数及总金额都是五位数，这两个五位数刚好由0～9这10个数码组成，即这两个五位数的所有数码互不相同。这些硬币的总金额最多是多少分？

　　34 甲、乙合伙买了一双冰鞋后，他俩带的钱还剩下30元，如果单独买这双冰鞋，那么甲差27元，乙差30.6元，这双冰鞋多少钱？

　　35 A，B，C，D四个钢珠，用天平两个两个称，共称了六次，最重的是B和C，第二重的是A和B。请将这四个钢珠按重量从重到轻依次排列出来。

　　36 A，B，C，D，E住在同一栋楼里，A住的高度是B的2倍、C的3倍、D的4倍、E的6倍，又已知C正好住在D的楼上。试判断他们各住在第几层。

　　37 汽车里程表表明汽车行驶了15951千米，这个数字从两面读都一样。汽车又行驶了3时后，里程表上的数字从两面读仍一样，并且在行驶途中还出现过一次这种情况。问：汽车这3时的平均速度是多少？

　　38 学校组织全校同学去春游，租用甲、乙两种大客车。若用7辆甲种大客车和4辆乙种大客车则需跑3趟，若用8辆甲种大客车和9辆乙种大客车则只需跑2趟（假设每辆车都满载）。甲、乙两种大客车哪种坐的乘客多？

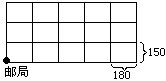
　　39 右图为某邮递员负责的邮区街道图，图中交叉点为邮户，每个小长方形的长为180米、宽为150米。如果邮递员每分行200米，在每个邮户停留半分，那么从邮局出发走遍所有邮户，再回到邮局，最少要用多少分？

　　40 一条公共汽车线路，包括首尾两站共10站。首尾两站同时每隔3分相向发车一辆，每辆汽车行驶一个单程需要27分。要保证首、尾两站随时都有车，至少需要多少辆汽车？

　　41 某路电车每隔5分从甲站发一辆电车到乙站，全程要走20分。有一个人从乙站出发沿电车线路前往甲站，他出发时恰有一辆电车到达乙站，在路上他又迎面遇到了10辆电车，到达甲站时恰有一辆电车从甲站开出。问：他从乙站到甲站用了多长时间？

　　42 一辆公共汽车在线路上行驶，包括起点站和终点站沿途共有10个站。如果在每个车站上车的乘客，在以后的每个站恰好都有1人下车，那么共有多少位乘客乘坐了这辆车？

　　43 长途汽车在甲、乙两地间运行，每天从甲、乙两地同时相对开出一辆客车，单程需要三天时间，到达终点后，休整两天再按原路返回。为了保证这条线路上客运任务能正常进行，这条线路上至少应配备几辆客车？

　　44 长途汽车有甲、乙两个终点站，汽车要用4时才能驶完全程。从上午6点开始，每隔1时从甲、乙两站同时发出一辆公共汽车，最后一班车在下午4点发出。问：从甲站发车的汽车司机最多能看到几辆迎面驶来的公共汽车？最少能看到几辆？

　　45 一个圆的周长是5.4米，两只蚂蚁从一条直径的两端同时出发沿圆周相向爬行，这两只蚂蚁每秒钟分别爬行5.5厘米和3.5厘米。它们每次爬行1秒、3秒、5秒……（连续奇数）就调头爬行。两只蚂蚁第一次相遇时，已爬行了多长时间？

　　46 马戏团的“猴子骑车”节目是由5只猴子用5辆自行车表演的，每只猴子至少骑一次车，但一只猴子不能重复骑同一辆车。表演结束后，5只猴子分别骑了2，2，3，5，x次，五辆车分别被骑了1，1，2，4，y次，求x＋y。

　　47 A，B两地相距54千米，有18人共同骑7匹马由A地到B地去，每匹马每次只能驮1人，为了轮换休息，大家决定每人骑马行1千米轮换一次。问：每人骑马、步行各多少千米？

　　48 一次象棋比赛共有10名选手参加，他们分别来自甲、乙、丙三个队。每个人都与其余9名选手各赛一盘，每盘棋的胜者得2分，负者得0分，平局各得1分。比赛结果，甲队选手平均得9分，乙队选手平均得7.2分，丙队选手平均得18分。甲、乙、丙队参赛选手各有几人？

　　49 四名棋手进行循环赛，胜一局得2分，平一局得1分，负一局得0分。比赛结果，没有人全胜，并且各人的总分都不相同。问：至多有多少局平局？

　　50 一次校友聚会有47人参加，在参加聚会的同学中有个有趣的现象，每个女生认识的男生人数各不相同，并恰好构成一串连续的自然数，最多的全认识，最少的也认识18个。问：这次聚会有多少个女生参加？

　　51 甲、乙、丙、丁四人出同样多的钱合伙买回一批本，分本时甲比其他三人各少拿了8个本，因而这三人分别退给甲0.70元。求每个本多少钱。

　　52 四个小朋友分20块糖，四人分到的糖数各不相同。分到糖数最多的小朋友至少能分到几块糖？

　　53 7个人共有100元钱，他们的钱数各不相同（均为整数元），试证明他们中至少有3人的钱数之和不少于50元。

　　54 有一个吹泡机，一次恰好吹出100个肥皂泡。肥皂泡吹出后，经过12％，这些肥皂泡不到4分钟全部破了。如果吹泡机每分钟吹一次，那么到第10次吹出新的肥皂泡时，没有破的肥皂泡至多有多少个？

　　55 甲、乙、丙和一些同学围坐在一张大圆桌旁。如果从甲开始数起，那么顺时针方向的第13人是乙，逆时针方向的第15人是丙；另外，乙是从丙开始数起，顺时针方向的第7人。问：圆桌旁总共坐有多少人？

　　56 A，B，C，D，E，F，G七人每月都要在一张圆桌上共餐几，但他们对安排座位有个规定，一个月中每个人只能与另外六个人中的每一人相邻一次。按照这个规定，一个月中这七个人至多能坐在一起共餐几次？

　　57 小明从1999年的日历中抽出14张，是从5月14日到5月27日连续14天的，这14天的日期数相加是287。小亮也抽出14张，也是连续的14天，这14天的日期数虽然与小明的不相同，但相加恰好也是287。小亮抽出的14张是从几月几日到几月几日？

　　58 某校毕业生共分9个班，每班人数相等。已知一班的男生比二、三两个班的女生总数多1；四、五、六三个班的女生总数比七、八、九三个班的男生总数多1。求该校毕业生中男、女生人数的比。

　　59 桌上放有345枚正面朝下的硬币，第1次翻动其中1枚，第2次翻动其中2枚，第3次翻动其中3枚……第345次翻动345枚。经过345次翻动后，能否使这345枚硬币都正面朝上？

　　60 若干个同样的盒子排成一排，小明把50多个同样的棋子分装在盒中，其中只有一个盒子没装棋子。小光趁小明不在时偷偷从每个有棋子的盒子中各拿了一个棋子放在空盒中，然后把盒子重新排了一下。小明回来后仔细查看一番，没发现有人动过这些盒子和棋子。问：共有多少个盒子？

　　61 一只用黑、白两种颜色的皮子缝制成的足球如右图所示。已知这只足球上有黑色皮子12块。问：这只足球上缝了多少块白色皮子？

　　62 甲定于下午3时乘飞机到达机场，乙驾车准时到机场去接，不料飞机早到达1时，甲信步由机场沿公路向单位走去，中途遇到乙，随即乘车返回单位，结果比原来计划提前10分到单位。问：甲下飞机信步走了多长时间？