整除性

　　75°如果四位数6□□8能被73整除，那么商是多少？

　　76°如果四位数5□□6能被34整除，那么可以有多少个不同的商？

　　77 个位数是6，且能被3整除的四位数有多少个？

　　78 三个数的和是555，这三个数分别能被3，5，7整除，而且商都相同，求这三个数。

　　

　　80 求各位数字都是 7，并能被63整除的最小自然数。

　　81 用1，2，3，4这四个数码可以组成24个没有重复数字的四位数，其中能被11整除的有哪些？

　　82 从 2，3，5，7，8五个数中任选四个能组成哪些能被75整除的没有重复数字的四位数？

　　83 一个三位数能被11整除，去掉末位数字后所得的两位数能被9整除，这样的三位数有哪些？

　　84 求出能被11整除，首位数字是4，其余各位数字均不相同的最大和最小的六位数。

　　85 已知自然数2*3*4*5*1能被11整除，问：*代表数码几？

　　86 已知四位数 7**1能被9整除，问：*代表数码几？

　　

　　88 把一个三位数的百位和个位上的数字互换，得到一个新的三位数，新、旧两个三位数都能被4整除。这样的三位数共有多少个？

　　89 在 8264的左右各添一个数码，使新得到的六位数能被45整除。

　　

　　91 在 666后面补上三个数码组成一个六位数，使这个六位数能被783整除，应当怎样补？

　　92 在 5678这个数的前面或后面添写一个数 2，所得到的两个五位数都能被2整除。现在请你找出一个三位数添写在5678的前面或后面，使所得的两个七位数都能被这个三位数整除。满足题意的三位数有哪几个？

　　93 一个四位数，四个数字各不相同，且是17的倍数，符合条件的最小四位数是多少？

　　94 一个自然数与19的乘积的最后三位数是321，求满足此条件的最小自然数。

　　95 一个整数乘以17后，乘积的后三位是999，求满足题意的最小整数。

　　96 1×2×3×…×15能否被 9009整除？

　　97 A=61×62×63×…×87×88，A能否被6188整除？

　　98 从1～ 9这九个数中选出六个不同的数字组成一个能被11整除的六位数，求出这样的六位数中最大的与最小的两数之和。

　　99 用1～ 9这九个数码组成一个没有重复数字的能被11整除的九位数，这样的九位数有31680个，求出其中最大的和最小的。

　　101 能否用1， 2， 3， 4， 5， 6六个数码组成一个没有重复数字，且能被11整除的六位数？为什么？

　　102 用8个不同数码组成的八位数中，能被36整除的最小的数是几？

　　103 用1—9这九个数码各一次，组成三个分别能被7，9，11整除的三位数，并要求这三个数的和尽可能大。

　　104 将自然数N接写在任一个自然数的右面，得到的新数都能被N整除。例如将2写在任一自然数的右面，得到的新数都能被2整除。在1～100中，满足条件的自然数N有哪几个？

　　105 111…11是各位数字都是1的自然数，并且是7的倍数，求这样的数中最小的那个数。

　　

　　107 已知A是一个自然数，它是15的倍数，并且它的各个数位上的数码只有0和8两种。问：A最小是几？

　　

　　109 在三位数abc中， 2b＋c=12，求必定能整除这个三位数的最大自然数。

　　110 一个四位数减去它的各位数字的和得到19□9，□中的数字是几？

　　111 用1～9这九个数码各一次，组成三个能被9整除的三位数，要求这三个数的和尽可能大，求这三个数。

　　

　　A和B。

　　113 用1，3，5，7，9中的任意一个数与2，4，6，8中的任意一个数相乘，在所有不同的积中有多少个能被6整除？

　　114 在1～13中任意取两个不同的数相乘，可以得到许多不相等的乘积，在所有这些不同的乘积中有多少个能被6整除？

　　115☆有一个2000位的数A能被9整除，它的各位数字之和为a，a的各位数字之和为b，b的各位数字之和为c。c等于多少？

　　116☆已知自然数A的各个数位上的数码之和与3×A的各个数位上的数码之和相等，证明A必能被9整除。

　　117 小马虎买了72支同样的钢笔，可是发票不慎落水浸湿，单价已无法辨认，总价数字也不全，只能认出：□11.4□元(□表示不明数字)。你能帮助小马虎找出不明数字吗？

　　118 小明买了6支铅笔、 2支圆珠笔、 3本笔记本和7块橡皮，总共用去2元9角钱。已知圆珠笔3角9分1支，橡皮6分1块，售货员算错帐了吗？

　　119 商店里有六箱货物，分别重15，16，18，19，20，31千克，两个顾客买走了其中五箱。已知一个顾客买的货物重量是另一个顾客的2倍。问：商店剩下的一箱货物重多少千克？

　　120 有一水果店进了六筐水果，分别装着香蕉和桔子，重量分别为8，9，16，20，22和27千克。当天只卖出一筐桔子，在剩下的五筐中香蕉的重量是桔子重量的2倍。问：这天水果店进了多少千克香蕉？

　　121 55个苹果分给甲、乙、丙三人，甲的苹果个数是乙的2倍，丙最少但也多于10个。问：三人各得多少苹果？

　　122 四名学生做加法练习：任写一个六位数，把它的个位数字(不等于0)拿到这个数最左边一位数字的左边得到一个新的六位数，然后与原六位数相加，他们的得数分别为172535，568741，620708，845267，其中只有一名同学做对了。问：正确答案是几？

　　123 证明：任意两个连续奇数的和一定是4的倍数。

　　124 证明：任意两个连续偶数的乘积是8的倍数。

　　125 证明：任意三个连续偶数的和一定是6的倍数。

　　126 证明：任意三个连续奇数的和一定是3的倍数。

　　127 证明：任意三个连续自然数的乘积是6的倍数。

　　128 证明：任意两个自然数的和、差、积中，至少有一个能被3整除。

　　129 甲数比乙数大5，乙数比丙数也大5，试说明三数之和、三数之积都能被3整除。

　　130 至少给出多少个自然数，才能使给出的数中总能选出3个，使得它们的和是3的倍数。

　　131 证明：任何一个三位数，连着写两遍得到一个六位数，这个六位数一定能被7，11，13整除。

　　132 能不能将从1到10的各数排成一行，使得任意相邻的两个数之和都能被3整除？

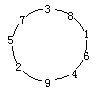
　　133☆1—9九个数字按右图所示的次序排成一个圆圈，请你在某两个数字之间剪开，分别按顺时针和逆时针次序形成两个九位数。如果要求剪开后所得到的两个九位数的差能被396整除，那么应在何处剪开？

　　

　　134 用六个2和若干个0组成的整数是否有可能是平方数？

　　135 11是平方数吗？为什么？

　　136 从1～1000中选出一些数，使得这些数中任意两个数的和都能被18整除。这样的数最多能选出多少个？