 南安市2003年秋季初二年数学科期末测查参考试卷(一)
南安市2003年秋季初二年数学科期末测查参考试卷(一)
(满分150分 考试时间120分)
| 题 号 | 一 | 二 | 三 | 总 分 | |||||||||||
| 1--8 | 9-18 | 19 | 20 | 21 | 22 | 23 | 24 | 24 | 25 | 26 | 27 | 28 | 29 | ||
| 得 分 | |||||||||||||||
一、选择题:相信自己,把每题的一个正确答案填入括号内(每题4分,共32分)。
1、下列计算正确的是( )
(A)a3+a2=a5 (B)a3·a2=a6 (C)(a3)2=a6 (D)(3a)3=3a3
2、下列图形中,既是轴对称图形,又是中心对称图形的是( )
(A)平行四边形 (B)等边三角形 (C)菱形 (D)梯形
3、已知: a>b,则下列各式中正确的是( )
(A)-3a>-3b (B)-a/3>-b/3 (C)3-a>3-b (D)a-3>b-3
4、一副扑克牌(去掉大小王),任意抽取其中一张是方块的机会是( )
(A)1/3 (B)1/4 (C)1/5 (D)13/54
5、要使正五边形旋转后,与自身重合,至少应将它绕中心逆时针方向旋转( )
(A)30º (B)45º (C)60º (D)72º


 6、如图(1)是国际奥林匹克运动会会旗的标志图案,它由五个半径相同的圆组成的,象征着五大洲体育健儿,为发展奥林匹克精神而团结起来,携手拼搏,那么这个图案是( )图形。
6、如图(1)是国际奥林匹克运动会会旗的标志图案,它由五个半径相同的圆组成的,象征着五大洲体育健儿,为发展奥林匹克精神而团结起来,携手拼搏,那么这个图案是( )图形。
(A)

 旋转对称 (B)轴对称
图1
旋转对称 (B)轴对称
图1
(C)中心对称 (D)既是轴对称又是中心对称
7、如图(2)在矩形ABCD中,BE平分∠ABC,AB=5cm,DE=3cm,则矩形ABCD周长为( )
|
|
|
|
|
|
![]()
|
|
|
|
|
二、认真填一填,相信聪明的你一定可以把正确答案填入空格
(每题3分,共30分)。
9、“x、y两数的平方差不大于这两个数的积”,列不等式表示为__________________
10、因式分解:x2—1=___________
|
12、不等式组 X—3≤0的整数解为___________。
—X<2
13、在□ABCD中,∠A:∠B:∠C=1:5:1,则∠D=___________
14、在□ABCD中,对角线AC与BD交于点O,且AC=8cm,BD=12cm,BC=5cm,则△AOD周长__________
15、木工师傅用两条相等的长木条及两条相等的短木条制作了一个门框,如图(4),现在给你一条绳子,请你说出根据______________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
16、如图5,△ABC可看作△DEF平移得到的,则AB与DE
的关系是___________________
17、如图6,在等腰梯形ABCD中,DCAB,AD=BC,BD⊥AD,∠A=60º,则∠DBC=__________________
|
 |
|
|
|
|
|
|
|
| 1 | 1 | 1 | 1 | 1 | 1 |
|
| 图形个数 | 1 | 2 | 3 | 4 | 5 | 6 | …… | n—1 | n |
| 周长 | 6 | 8 | 12 | 14 | 18 |
三、沉着思考,冷静解答以下各题,(19—22每题7分,23—28每题8分,29题12分)。
19、计算:-12xy·3x2y - x2y(-3xy+1)
20、因式分解:4x3+8x2y+4xy2
21、解不等式,并把解集在数轴上表示出来:
![]() <1
<1
|
|
 |
|
|
|
|
23、小李与小明在掷一枚质量均匀的骰子,他们规定只掷一次,小李说:“若你掷到点数是6的你赢,否则我赢。”而小明说:“不,若你掷到的点数是1或2中的一种,那你赢,否则是我赢。”
问:(1)你认为他们的规则对两人公平吗?请说明理由。
(2)请你设计一种方案,在其他条件不变的情况下,使两人赢的机会均等。
24、已知:ax·a8=a11,(ax)y= a6,请先化简后求(x+y)(x—y)—(x+y)2的值。
 25、某中学有若干名学生住宿舍,每间住5人,则有20人没宿舍住,若每间住8人,则有一间没住满,但超过一半,求学生宿舍有多少间?学生人数有多少人?
25、某中学有若干名学生住宿舍,每间住5人,则有20人没宿舍住,若每间住8人,则有一间没住满,但超过一半,求学生宿舍有多少间?学生人数有多少人?
26、已知:四边形ABCD中,对角线AC与BD交于点O,且AC⊥BD,
(1)试说明四边形ABCD的面积S=![]() AC·BD;
AC·BD;
(2)当O是AC中点,O是BD中点时,请说明四边形ABCD是菱形。
 |

|
|
|
|
|
27 、设计与制作
1、画出△ABC沿东偏南30º方向平移距离4cm的图形△A′B′C′
 |
|
|
B
2、请你运用所学的知识,在下面方框中设计一个既是中心对称图形,
又是轴对称图形的图案,并为你的图案取一个标题。
 |
|
标题:
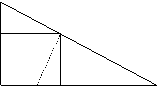
28、如图,已知:直角△ABC中,∠C=90º,DE⊥BC,△AED是图中的∠A′FD绕D点旋转90º得到的图形,试说明:
(1)四边形DECF是正方形;
(2)若AD=3cm,BD=6cm,求△BDF与△ADE的面积之和。
|
 |
|
|
|
|
|
|
29、实践探索题:
(1)拼一拼,画一画:
|
|
你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多39cm2,求小正方形的边长。